Search fundamentals
The ability to plan before acting is a hallmark of intelligence. Before going on a trip to a different country, before starting a new project, before writing functions in code, we plan. Planning happens at different levels of detail to strive for the best possible outcome when carrying out the tasks involved to accomplish goals.
Plans rarely work out perfectly in the way that we envision at the start. We live in a world where things are constantly changing, so it is impossible to account for all the variables and unknowns along the way. Regardless of the plan we started with, we almost always deviate. We need to (again) make a new plan from our current point going forward as unexpected events occur. As a result, the final plan that is carried out is usually quite different from the original one.
Searching is a way to guide planning by creating steps in a plan. When we plan a trip, for example, we search for routes to take, evaluate the stops along the way and what they offer, and search for accommodations and activities that we like and can afford. Depending on the results of these searches, the plan changes.
One scenario where search algorithms are useful is finding the shortest path to the goal in a maze. Suppose that we’re in a square maze that is 10 blocks by 10 blocks. There’s a goal that we want to reach and barriers that we cannot step into or over. The objective is to find a path to the goal while avoiding barriers with as few steps as possible by moving north, south, east, or west. In this example, the “player” cannot move diagonally.
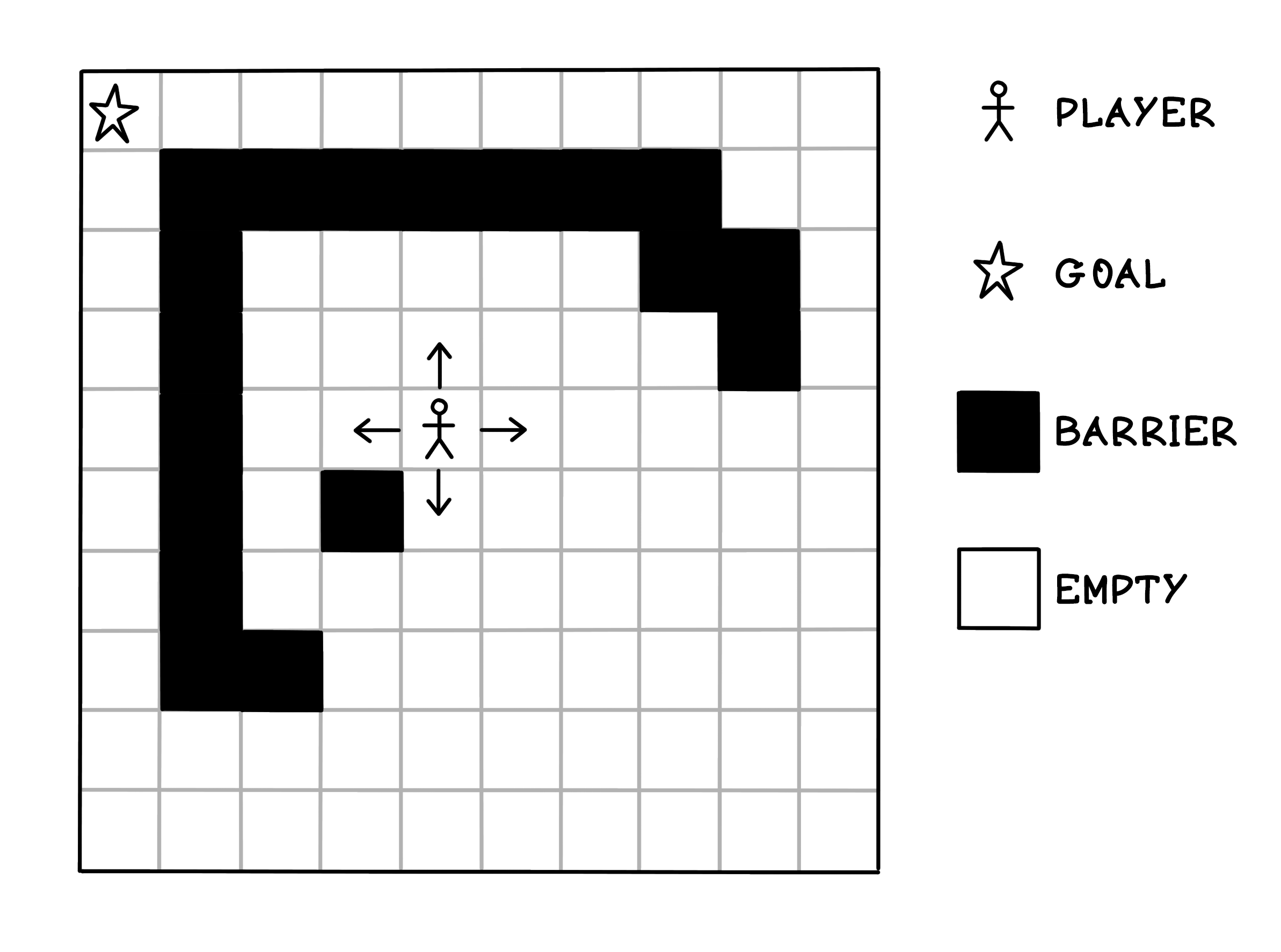
Uninformed search is also known as unguided search, blind search, or brute-force search. Uninformed search algorithms have no additional information about the domain of the problem apart from the representation of the problem, which is usually a tree.
Breadth-first search
Breadth-first search is an algorithm used to traverse or generate a tree. This algorithm starts at a specific node, usually the root, and explores every node at that depth before exploring the next depth of nodes. Think of BFS like dropping a stone into a calm pond. The ripples expand uniformly in all directions, touching everything 1 meter away, then everything 2 meters away, and so on. The algorithm mimics this expanding ring, visiting all neighbors at the current depth before moving outward. This guarantees finding the shortest path in unweighted graphs (graphs where all edges have the same cost).
Depth-first search
Depth-first search is another algorithm used to traverse a tree or generate nodes and paths in a tree. Think of DFS like a maze explorer who commits to a single path, walking as far as possible until hitting a dead end. Only then do they backtrack to the last intersection to try a different turn. Unlike the cautious, expanding nature of BFS, DFS is aggressive and dives deep immediately.
When BFS and DFS shine
BFS is a great fit when the shortest path actually matters and when the branching factor is still manageable. That is why BFS is often taught first for routing, puzzle solving, and other problems where every step has the same cost. DFS becomes attractive when memory is limited or when we simply need to find a solution rather than the best one. The tradeoff is that DFS can wander far down an unhelpful path before it learns that it needs to backtrack.
Play with a search simulation
The simulation below illustrates the difference between BFS and DFS. The agent attempts to find the goal in the maze using both algorithms. You can tap Reset to start a new simulation with a random maze. Play with choosing different goals in the maze to see how the algorithms perform by tapping on the maze grid.
This toy maze keeps the rules simple on purpose: every move costs the same, there are no diagonal moves, and the world is fully visible. Real search problems often add weighted costs, partial information, time pressure, or huge graphs. That is where the deeper ideas in the book start to matter even more.
Breadth-first search (BFS)
Explores in expanding waves to guarantee the shortest path.
Depth-first search (DFS)
Dives deep quickly, then backtracks to explore alternatives.
Grokking AI Algorithms
How AI solves complex problems
A practical, visual guide to the algorithms that power search, machine learning, neural networks, LLMs, and generative AI.
Search Fundamentals Frequently Asked Questions (FAQ)
What is breadth-first search in AI?
Breadth-first search, or BFS, explores all nearby options before moving deeper. It is especially useful when you want the shortest path in an unweighted graph or maze.
What is depth-first search in AI?
Depth-first search, or DFS, follows one path as far as it can before backtracking. It can be simpler and more memory-efficient than BFS, but it does not guarantee the shortest path.
What is the main difference between BFS and DFS?
The main difference is exploration order. BFS expands layer by layer from the start, while DFS commits to one branch at a time before retreating and trying another.
Does BFS always find the shortest path?
BFS finds the shortest path in terms of number of steps when all edges have equal cost. That is why it performs so well in simple maze and graph problems like the simulation in this chapter.
Does DFS always use less memory than BFS?
DFS often uses less memory because it does not need to store an entire frontier of nearby nodes at once. However, the exact memory cost still depends on the structure of the graph or maze.
When should I use BFS instead of DFS?
Use BFS when path quality matters, especially when you need the shortest route. Use DFS when memory is tighter, when you want a fast way to explore deep branches, or when the problem structure makes exhaustive shortest-path guarantees less important.
Why can DFS get stuck exploring a poor path?
DFS commits early to one branch and keeps going until it hits a dead end or a stopping condition. If the first branch is not promising, it may spend time exploring deeply before trying a better route elsewhere.
What is a frontier in search algorithms?
The frontier is the collection of states discovered but not yet explored. In BFS it behaves like a queue, while in DFS it behaves more like a stack.
Why are graphs important in search problems?
Many problems can be modeled as graphs, where nodes represent states or locations and edges represent possible transitions. Once a problem is expressed as a graph, search algorithms can systematically explore it.
What real-world systems use BFS or DFS ideas?
Pathfinding, dependency analysis, network traversal, puzzle solving, route planning, and many AI planning tasks all rely on search patterns closely related to BFS and DFS.
What does the maze simulation help you understand?
It makes the tradeoff visible. Instead of reading abstract definitions, you can see how different exploration orders change visited cells, frontier growth, and the path that is eventually found.